Aleksey Shipilёv, @shipilev, aleksey@shipilev.net
|
Caution
|
This is a very long transcript for a very long talk. The talk’s running time is close to 120-150 minutes, and transcript may take even longer if digested thoughtfully. Please plan your reading accordingly. There are five large sections which are mostly independent of each other, that should help to split the reading. |
|
Warning
|
The talk is correct to the best of my knowledge, but parts of it may still be incorrect, misguided, or sometimes wrong. The only true source of truth is The Java Language Specification itself. My understanding of JMM was proven incorrect more than once over the previous five years. If you see something wrong in the post, don’t hesitate to drop me a note. |
Preface
The Java Memory Model is the most complicated part of Java spec that must be understood by at least library and runtime developers. Unfortunately, it is worded in such a way that it takes a few senior guys to decipher it for each other. Most developers, of course, are not using JMM rules as stated, and instead make a few constructions out of its rules, or worse, blindly copy the constructions from senior developers without understanding the limits of their applicability. If you are an ordinary guy who is not into hardcore concurrency, you can pass this post, and read high-level books, like "Java Concurrency in Practice". If you are one of the senior folks interested in how all this works, read on!
This post is a transcript of the "Java Memory Model Pragmatics" talk I gave during this year at different conferences, mostly in Russian. There seems to be a limited supply of conferences in the world which can accommodate such a long talk, and being in need for exposing some background reading for my JMM Workshop at JVMLS this year, I decided to transcribe it.
We will reuse a lot of the slides, and I’ll try to build the narrative based on them. Sometimes I’ll just skip over without narrative when the slides are self-explanatory. The slides are available in Russian and English. The slides below are rasterized, but have a nice native resolution. Zoom-in if they are unreadable. Sane browsers smartly resize the images, and more details are visible when zoomed in. (I would make the illustrations in SVG, but my iPad crashes when trying to render 150+ of them on one page!)
I would like to thank Brian Goetz, Doug Lea, David Holmes, Sergey Kuksenko, Dmitry Chyuko, Mark Cooper, C. Scott Andreas, Joe Kearney and many others for helpful comments and corrections. The example section on final fields contains the info untangled by Vladimir Sitnikov and Valentin Kovalenko, and is the excerpt from their larger talk on Final Fields Semantics.
Intro
First, a simple detector slide. Hey there, @gakesson, waves!
If you read just about any language spec, you will notice it can be logically divided into two related, but distinct parts. First, a very easy part, is the language syntax, which describes how to write programs in the language. Second, the largest part, is the language semantics, which describes exactly what a particular syntax construct means. Language specs usually describe the semantics via the behavior of an abstract machine which executes the program, so the language spec in this manner is just an abstract machine spec.
When your language has storage (in the form of variables, heap memory, etc.), the abstract machine also has storage, and you have to define a set of rules concerning how that storage behaves. That’s what we call a memory model. If your language does not have explicit storage (e.g. you pass the data around in call contexts), then your memory model is darn simple. In storage-savvy languages, the memory models appear to answer a simple question: "What values can a particular read observe?"
In sequential programs, that seems a vacuous question to ask: since you have the sequential program, the stores into memory are coming in some given order, and it is obvious that the reads should observe the latest writes in that order. That is why people usually meet with memory models only for multi-threaded programs, where this question becomes complicated. However, memory models matter even in the sequential cases (although they are often cleverly disguised in the notion of evaluation order).
For example, the infamous example of undefined behavior in a C program that packs a few increments between the sequence points. This program can satisfy the given assert, but can also fail it, or otherwise summon nasal demons. One could argue that the result of this program can be different because the evaluation order of increments is different, but it would not explain, e.g. the result of 12, when neither increment saw the written value from the other. This is the memory model concern: what value should each increment see (and by extension, what it would store).
Either way, when presented with a challenge of implementing the particular language, we can go one of two ways: interpretation, or compilation of abstract machine to the target hardware. Both interpretation and compilation are connected via Futamura Projections anyway.
The practical takeaway is that both interpreter and compiler are tasked with emulating the abstract machine. Compilers are usually blamed for screwing up the memory models and multi-threaded programs, but interpreters are not immune, either. Failing to run an interpreter to the abstract machine spec may result in memory model violations. The simplest example: cache the field values over volatile reads in an interpreter, and you are done for. This takes us to an interesting trade-off.
The very reason why programming languages still require smart developers is the absence of hypersmart compilers. "Hyper" is not a overstatement: some of the problems in compiler engineering are undecidable, that is, non-solvable even in theory, let alone in practice. Other interesting problems may be theoretically feasible, but not practical. Therefore, to make practical (optimizing) compilers possible, we need to cause some inconvenience in the language. The same goes for hardware, since (at least for Turing machines) it is just the algorithms in silica.
To elaborate on this thought, the rest of the talk is structured as follows.
Part I. Access Atomicity
What Do We Want
The simplest thing to understand in JMM is the access atomicity guarantee. To specify this more or less rigorously, we need to introduce a bit of notation. In the example on this slide, you can see the table with two columns. This notation reads as follows. Everything in the header happened already: all variables are defined, all initializing stores committed, etc. The columns are different threads. In this example, Thread 1 stores some value V2 into global variable t. Thread 2 reads the variable, and asserts the read value. Here, we want to make sure the reading thread only observes the known value, not some value in between.
What Do We Have
This seems to be a very obvious requirement for a sane programming language: how you can possibly violate this, and why? Here is why.
To maintain atomicity under concurrent accesses, you have to at least have the machine instructions operating with the operands of given width, otherwise the atomicity is broken on instruction level: if you need to split the accesses into several sub-accesses, they can interleave. But even if you have the desired-width instructions, they still can be non-atomic: for example, the atomicity guarantees for 2- and 4-byte reads are unknown for PowerPC (they are implied to be atomic).
Most platforms, however, do guarantee atomicity for up to 32-bit accesses. This is why we have a compromise in JMM which relaxes the atomicity guarantees for 64-bit values. Of course, there are still ways to enforce atomicity for 64-bit values, e.g. by pessimistically acquiring the lock on update and read, but that will come at a cost, and so we provide an escape hatch: users put volatile where they need atomicity, and VM and hardware work together to preserve it, no matter what the costs are.
On most hardware it is not enough, however, to have the desired-width operations to maintain atomicity. For example, if data access causes multiple transactions to memory, the atomicity is off, even though we executed a single access instruction. In x86, for example, the atomicity is not guaranteed if the read/write spans two cache lines, since it requires two memory transactions. This is why generally only the aligned reads/writes are atomic, which forces VMs to align the data.
In this example, which is printed by JOL, we can see the long field being allocated at offset 16 from the object start. Coupled with object alignment of 8 bytes, we have the perfectly aligned long. Now, it would not violate the memory model to put long at offset 12, if we know it is not volatile, but that will only work on x86 (other platforms may violently disagree on performing misaligned accesses), and possibly with performance disadvantages.
Test Your Understanding
Let’s test our understanding with a simple quiz. Setting -1L is equivalent to setting all the bits to 1 in long.
Answer (select over to reveal): No magic is involved; a volatile long field inside AtomicLong guarantees this. This is required by the language spec, and no special treatment for AtomicLong from the VM side is needed for this sample to work.
Value Types and C/C++
In Java, we are "lucky" to have the built-in types of small widths. In other languages which provide value types, the type width is arbitrary, which presents interesting challenges for the memory model.
In this example, C++ follows C compatibility by supporting structs. C++11 additionally supports std::atomic, which requires access atomicity for every Plain Old Data (POD) type T. So, if we do a trick like this in C++11, the implementations are forced to deal with atomically writing and reading the 104-byte memory blocks. There are no machine instructions which can guarantee atomicity at these widths, so implementation should resort to either CAS-ing, or locking, or something else.
(It gets even more interesting since C++ allows separate compilation: now the linker is tasked with the job of figuring out what locks/CAS-guards are used by this particular std::atomic. I am not completely sure what happens if threads execute the code generated by different compilers in the example above.)
JMM Updates
This section covers the atomicity considerations for the updated Java Memory Model. See a more-thorough explanation in a separate post.
In 2014, do we want to reconsider the 64-bit exception? There are few use cases when racy updates to long and double make sense, e.g. in scalable probabilistic counters. Developers may reasonably hope the long/double accesses are atomic on 64-bit platforms, but they nevertheless require volatile to be portable if the code is accidentally run on 32-bit platforms. Marking fields volatile will pay the cost of memory barriers.
In other words, since volatile is overloaded with two meanings: a) access atomicity; and b) memory ordering — you cannot get one without getting the other as baggage. One can speculate on the costs of removing the 64-bit exception. Since VMs are handling access atomicity separately by emitting special instruction sequences, we can hack the VM into unconditionally emitting atomic instruction sequences when required.
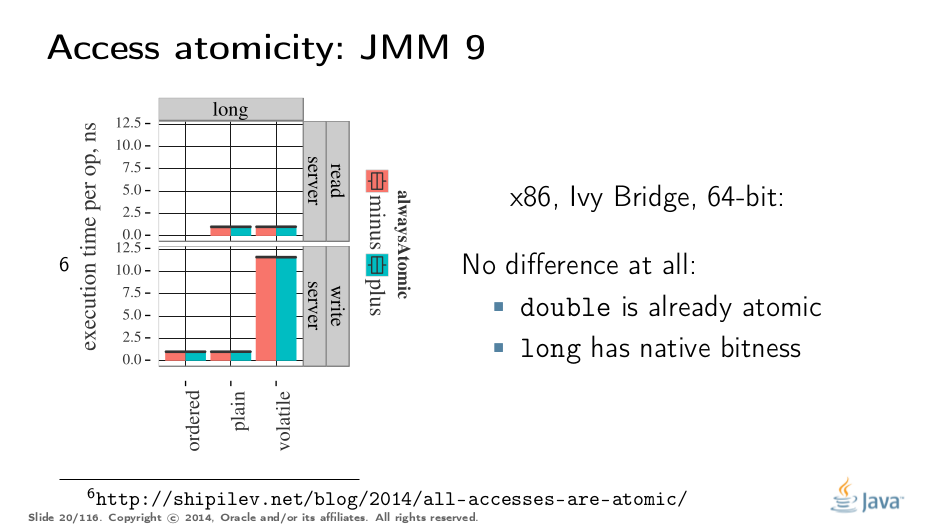
It takes some time to understand this chart. We can measure reads and writes of longs — three times for each access mode (plain, volatile, and via Unsafe.putOrdered). If we are implementing the feature correctly, there should be no difference on 64-bit platforms, since the accesses are already atomic. Indeed there is no difference between the colored bars on 64-bit Ivy Bridge.
Notice how heavyweight a volatile long write can be. If I only wanted atomicity, I pay this cost for memory ordering.
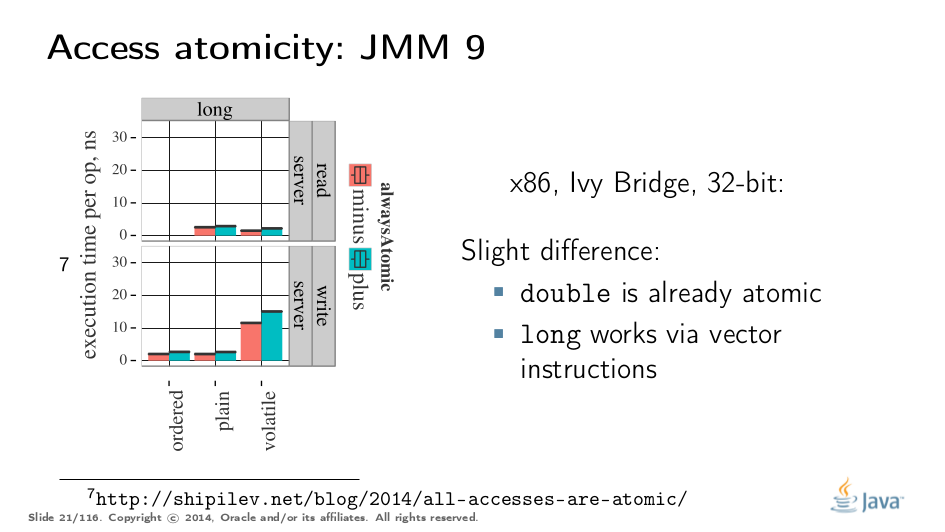
It gets more complicated when dealing with 32-bit platforms. There, you will need to inject special instruction sequences to get the atomicity. In the case of x86, FPU load/stores are 64-bit wide even in 32-bit platforms. You pay the cost of "redundant" copies, but not that much.
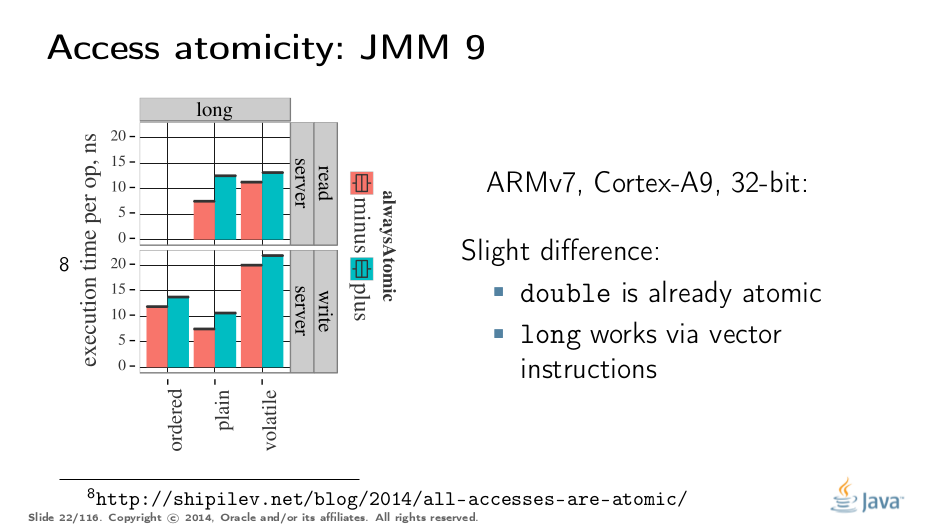
On non-x86 platforms, we also have to use alternative instruction sequences to regain atomicity, with predictable performance impact. Note that in this case, as well in the 32-bit x86 case, volatile is a bit slower with enforced atomicity, but that’s a systematic error since we need to also dump the values into a long field to prevent some compiler optimizations.
Part II. Word Tearing
What Do We Want
Word tearing is related to access atomicity.
If two variables are distinct, then the actions on them should also be distinct, and should not be affected by the actions on adjacent elements. How can this example break? Quite simple: if our hardware cannot access a distinct array element, it will be forced to read several elements, modify one element in the bunch, and then put the entire bunch back.
If two threads are doing the same dance on their separate elements, it might happen that another thread stores its own steps back to memory, overwriting an element updated by the first thread. This may and will cause lots of headaches for unsuspecting users, because without the clear provisions in the language spec, runtimes are free to apply transformations that can lead to hard-to-diagnose bugs.
What Do We Have
If we want to prohibit word tearing, we need hardware support for accesses of a given width. In the most simple scenario of a boolean[] array or a group of boolean fields, you can’t readily access a single memory bit on most hardware, since the lower addressability bound is usually a single byte.
Remarkably, you have to explain word tearing to programmers these days. Most of the systems programmers from days before are intimately familiar with it, and do understand the horror of chasing such a bug in a real system.
Therefore, Java, shooting to be a sane language, forbids word tearing. Period. Bill Pugh (FindBugs is his most attributed baby, but he was also the lead for JMM JSR 133) was quite articulate about that. I was chasing a word-tearing bug in a C++ program once — NOT FUN.
This requirement seems rather easy to fit with current hardware: the only data type you may care about is boolean, which you would probably want to take a full byte instead of single bits. Of course, you also need to tame any compiler optimizations which may buffer reads and writes along with the adjacent data.
Most people look to docs for an allowed range of primitive values and infer the machine-representation widths from there. You can only imply the minimum machine width to represent, say 2^64 cases for long. It does not oblige a runtime to actually allocate 8 bytes per long; it could, in principle, use 128-byte longs, as long as it’s practical for some weird reason.
However, most runtimes I know of are practical, and the machine representation widths closely fit the value domains, wasting no space. boolean, as I said before, is the only exception from this rule. JOL tries to figure out the actual machine widths, and you can see the scales on this slide. The numbers are the bytes taken by reference, boolean, byte, short, char, int, float, long, and double, respectively — exactly what we would expect them to be. Other platforms may be perceived… strange.
Test Your Understanding
Answer (select over to reveal): Any of (true, true), (false, true), (true, false), because BitSet stores the bits densely in long[] arrays and uses the bit magic to access a particular bit. Winning greatly in memory footprint, it breaks away from word-tearing guarantees of the language. (BitSet Javadocs say multi-threaded usages should be synchronized, so this is arguably an artificial example)
Layout Control and C/C++
Quite a few people want to control the memory layout for the particular class for a better footprint in marginal cases, and/or better performance. But in a language that allows an arbitrary layout for its variables, you cannot consistently forbid word tearing, because you would have to pay the price, as in this example.
There are no machine instructions that can write 7 bits at once, or read only 3 bits at once, so implementations would need to get creative if they are tasked with avoiding word tearing. C/C++11 allow you to use this sharp tool, but tell you that once you start, you are on your own.
JMM Updates
Nobody disputes that word tearing should remain forbidden.
Part III: SC-DRF
What Do We Want
Now we are getting to the most interesting part of a memory model: reasoning about program reads at large. It would be natural to think that programs are executing their statements in some global order, sometimes switching between the threads. This is a really simple model, and Lamport has defined it for us already: sequential consistency.
Notice the highlight. Sequential consistency does not mean the operations were executed in a particular total order! (The stronger strict consistency provides that). It is only important that the result is indistinguishable from some execution which has the total order of operations. We call executions like these sequentially consistent executions, and their results are called sequentially consistent results.
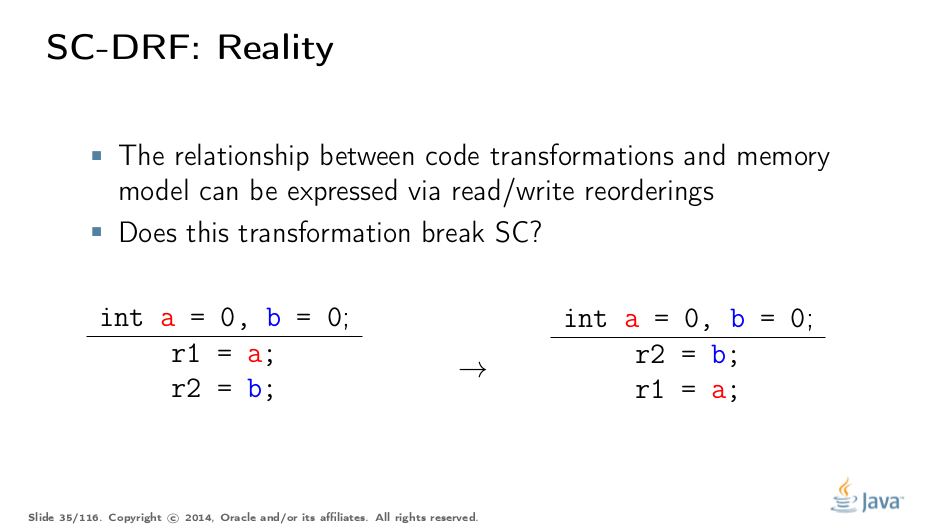
SC apparently gives us the opportunity to optimize the code. Since we are not bounded by actual total execution order, but only have to pretend to have one, we can have funny optimizations. For example, this program transformation does not break SC: there is obviously a SC execution of the original program which yields the same result (assuming nobody cares about the values of a and b anymore).
Notice that SC allows us to shrink the set of possible executions. At the extreme, we are free to choose a single order and stick to it.
What Do We Have
However, the optimizability under SC is overrated. Notice that current optimizing compilers, not to mention hardware, only care about the current instruction stream. So, if we have two reads in the instruction stream, can we reorder them as in this example and maintain SC?
Turns out, you can’t. If another part of a program stores the values into a and b, then read reordering breaks SC. Indeed, the original program executing under SC can only have the results matching (*, 2) or (0, *), but the modified program, even executed in total order manner, yields (1, 0), baffling developers expecting SC from their code.
You see, then, to figure out whether even a very simple transformation is plausible, you need sophisticated analysis, which does not readily scale to realistic programs. In theory, we can have a smart global optimizer (GMO) that can perform this analysis. I think the existence of a GMO is closely tied to the existence of Laplace’s Demon :)
But since we don’t have a GMO, all optimizations are conservatively forbidden for fear of inadvertently violating SC, and that costs performance. So what? We can go without the transformation, right? Unlikely: even the very basic transformations would be forbidden. Think about it: can you put a variable on register if that effectively eliminates the reads elsewhere in the program, i.e. does reordering?
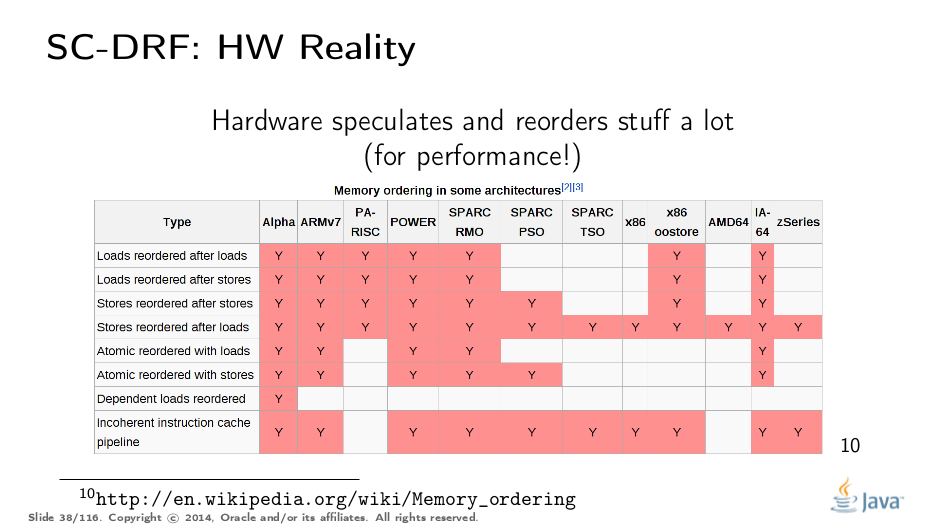
…and while we can forbid some of the optimizations in compilers to stop wreaking havoc in otherwise SC programs, hardware cannot be easily negotiated with. Hardware already reorders lots of stuff, and provides the costly escape hatches to intimidate reorderings ("memory barriers"). Therefore, a model which does not control what transformations are possible and what optimizations are encouraged would not realistically run with decent performance. For example, if we are to require sequential consistency in the language, we will probably have to pessimistically emit memory barriers around almost every single memory access, in order to slay hardware attempts at "optimizing".
Moreover, if your program contains races, current hardware does not guarantee any particular outcome from those conflicting operations. Hans Boehm and Sarita Adve stand firm on this.
Therefore, to accommodate the reality into the model with plausible performance, we need to weaken it.
Java Memory Model
This is where things get significantly more complicated. Since the language spec should cover all possible programs expressible in the language, we can’t really provide a finite number of constructions which are guaranteed to work: their union will leave white spots in semantics, and white spots are bad.
Therefore, the JMM tries to cover all possible programs at once. It does so by describing the actions which an abstract program can perform, and those actions describe what outcomes can be produced when executing a program. Actions are bound together in executions, which combine actions with additional orders describing the action relationships. This feels very ivory-tower-esque, so let’s get to the example right away.
Program Order
The very first order is Program Order (PO). It orders the actions in a single thread. Notice the original program, and one of the possible executions of this program. There, the program can read 1 from x, fall through to the else branch, store 1 to z, and then go on to read something from y.
Program order is total (within one thread), i.e. each pair of actions is related by this order. It is important to understand a few things.
The actions linked together in program order do not preclude being "reordered". In fact, it is a bit confusing to talk about reordering of actions, because one probably intends to speak of statement reordering in a program, which generates new executions. It will then be an open question whether the executions generated by this new program violate the provisions for JMM.
The program order does not, and I repeat, does not provide the ordering guarantees. The only reason it exists is to provide the link between possible executions and the original program.
This is what we mean. Given the simple schematics of actions and executions, you can construct an infinite number of executions. These executions are detached from any reality; they are just the "primordial soup", containing everything possible by construction. Somewhere in this soup float the executions which can explain a particular outcome of the given program, and the set of all such plausible executions cover all plausible outcomes of the program.
Here is where Program Order (PO) jumps in. To filter out the executions we can take to reason about the particular program, we have intra-thread consistency rules, which eliminate all unrelated executions. For instance, in the example above, while the illustrated execution is abstractly possible, it does not relate to the original program: after reading 2 from x, we should have written 1 to y, not to z.
Here is how we can illustrate this filtering. Intra-thread consistency is the very first execution filter, which most people do implicitly in their heads when dealing with JMM. You may notice at this point that JMM is a non-constructive model: we don’t build up the solution inductively, but rather take the entire realm of executions, and filter out those interesting to us.
Synchronization Order
Now we begin to build the part of the model which really orders stuff. In weak memory models, we don’t order all the actions, we only impose a hard order on a few limited primitives. In the JMM, those primitives are wrapped in their respective Synchronization Actions.
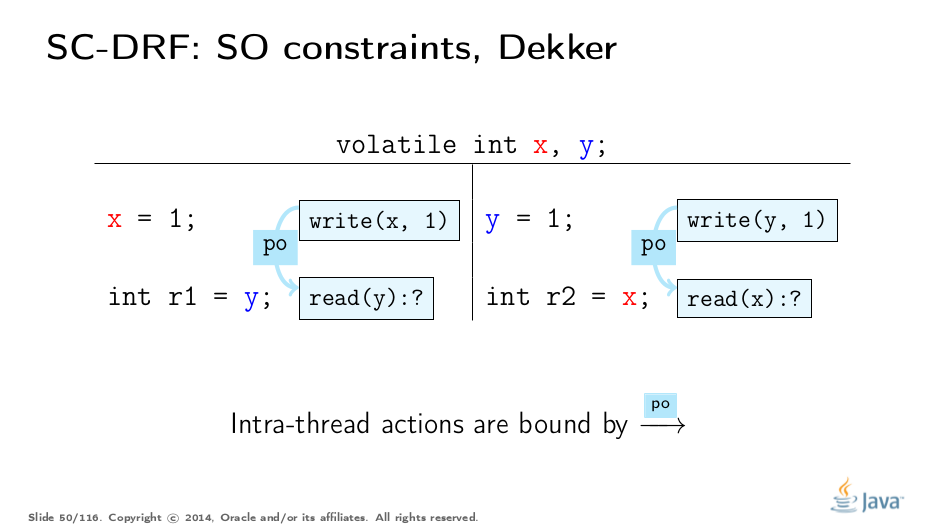
Synchronization Order (SO) is a total order which spans all synchronization actions. But this is not the most interesting part about this order. The JMM provides two additional constraints: SO-PO consistency, and SO consistency. Let’s unpack these constraints using a trivial example.
This is a rather simple example derived from the Dekker Lock. Try to think what outcomes are allowed and why. After that, we’ll move on to analyzing it with the JMM.
The slides below are self-explanatory, and we’ll just skip them over:
Now if we look at these rules more closely, we’ll notice an interesting property. SO-PO consistency tells us that the effects in SO are visible as if the actions are done in program order. SO consistency tells us to observe all the actions preceding in the SO, even those that happened in a different thread. It is as if SO-PO consistency tells us to follow the program, and SO consistency allows us to "switch between threads" with all effects trailing us. Mixed with the totality of SO, we arrive at an interesting rule:
Synchronization Actions are sequentially consistent. In a program consisting of volatiles, we can reason about the outcomes without deep thinking. Since SAs are SC, we can construct all the action interleavings, and figure out the outcomes from there. Notice there is no "happens-before" yet; SO is enough to reason.
IRIW is another good example of SO properties. Again, all operations yield synchronization actions. The outcomes may be generated by enumerating all the interleavings of program statements. Only a single quad is forbidden by that construction, as if we observed the writes of x and y in different orders in different threads.
The real takeaway was best summed up by Hans Boehm. If you take an arbitrary program, no matter how many races it contains, and sprinkle enough volatile-s around that program, it will eventually become sequentially consistent, i.e. all the outcomes of the program would be explained by some SC execution. This is because you will eventually hit a critical moment when all the important program actions turn into synchronization actions, and become totally ordered.
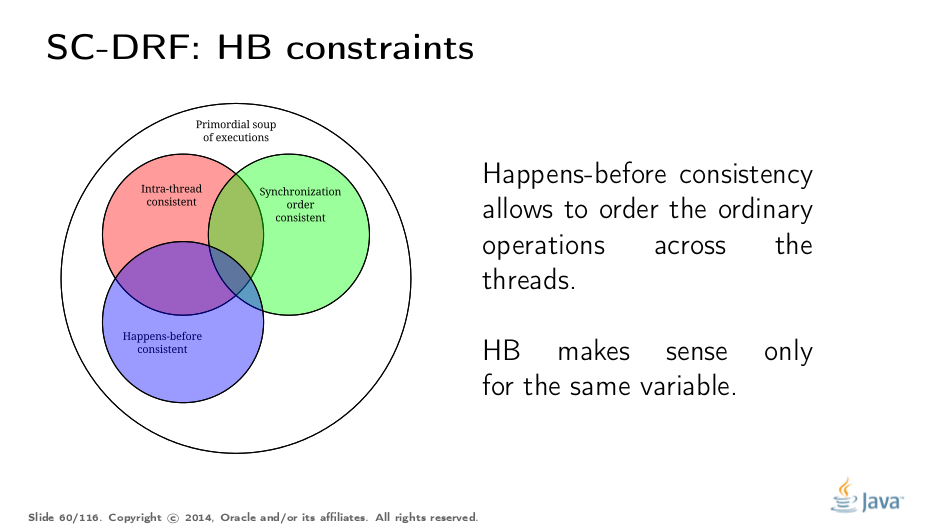
To conclude with our Venn diagram, SO consistencies filter out the executions with broken synchronization "skeletons". The outcomes of all the remaining executions can be explained by program-order-consistent interleavings of synchronization actions.
Happens-Before
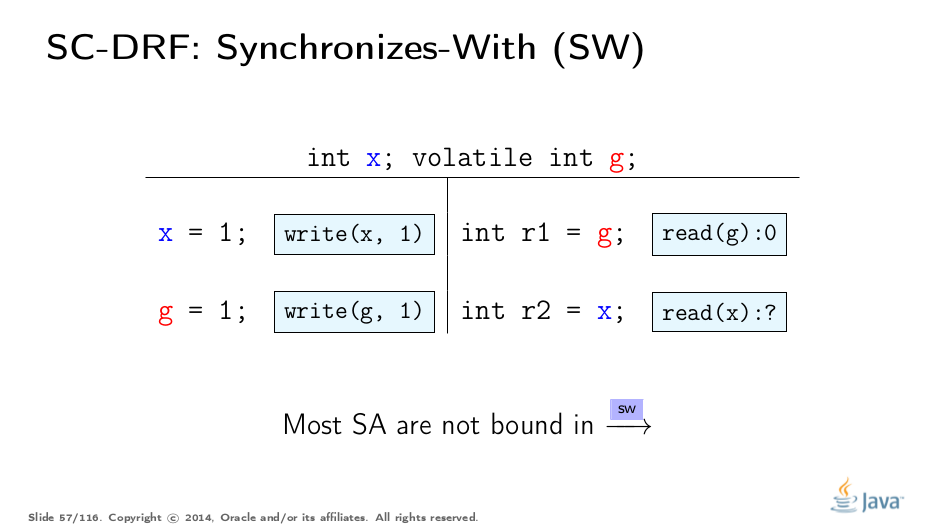
While providing a good basis to reason about programs, SO is not enough to construct a practical weak model. Here is why.
Let us analyze a simple case. Given all we learned so far about SO, do we know if (1, 0) outcome is allowed?
Let’s see. Since SO only orders the actions over g, nothing prevents us from reading either 0 or 1 from x. Bad…
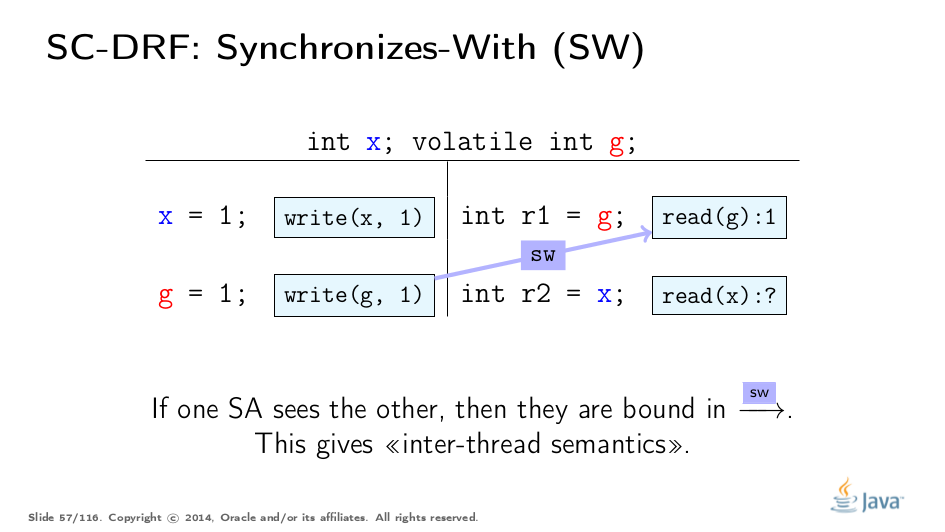
We need something to connect the thread states, something which will drag the non-SA values along. SO is not usable for that, because it is not clear when and how it drags the state along. So, we need a clear-cut suborder of SO which describes the data flow. We call this suborder synchronizes-with order (SW).
It is rather easy to construct SW. SW is a partial order, and it does not span all the pairs of synchronization actions. For example, even though two operations on g on this slide are in SO, they are not in SW.
SW only pairs the specific actions which "see" each other. More formally, the volatile write to g synchronizes-with all subsequent reads from g. "Subsequent" is defined in terms of SO, and therefore because of SO consistency, the write of 1 only synchronizes-with with reads of 1. In this example, we see the SW between two actions. This suborder gives us the "bridge" between the threads, but applying to synchronization actions. Let’s extend this to other actions.
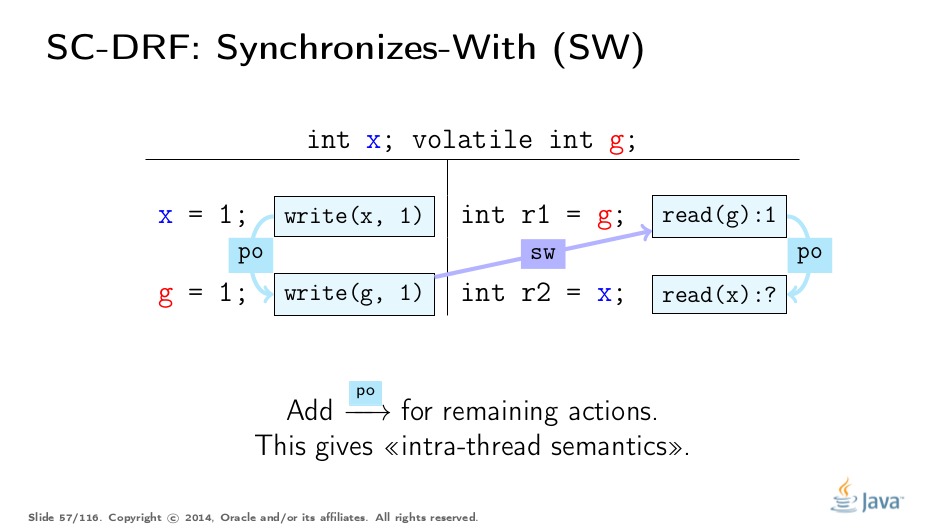
Intra-thread semantics are described by Program Order. Here it is.
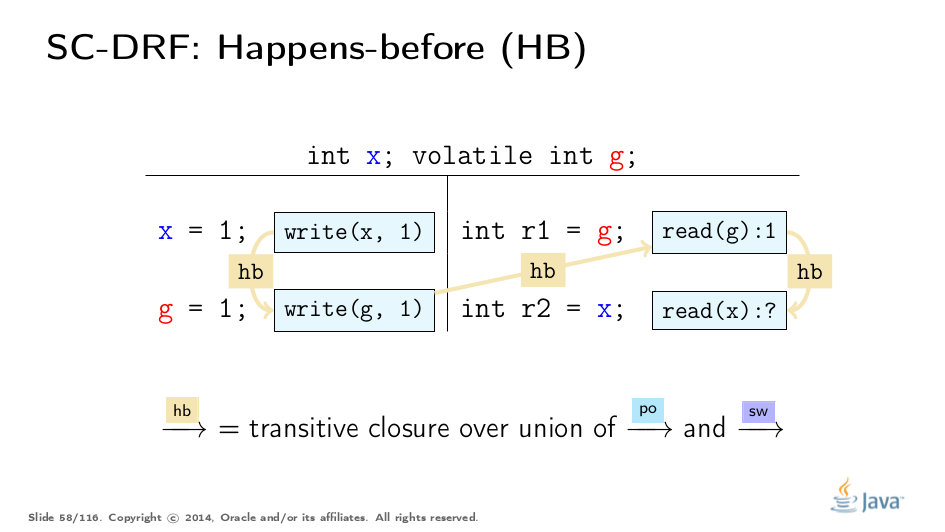
Now, if we construct the union of PO and SW orders, and then transitively close that union, we get the derived order: Happens-Before (HB). HB in this sense acquires both inter-thread and intra-thread semantics. PO leaks the information about sequential actions within each thread into HB, and SW leaks when the state "synchronizes". HB is partial order, and allows for construction of equivalent executions with reordered actions.
Happen-before comes with yet another consistency rule. Remember the SO consistency rule, which stated that synchronization actions should see the latest relevant write in SO. Happens-before consistency is similar in application to HB Order: it dictates what writes can be observed by a particular read.
HB consistency is interesting in allowing races. When no races are present, we can only see the latest preceding write in HB. But if we have a write unordered in HB with respect to a given read, then we also can see that (racy) write. Let’s define it more rigorously.
The first part is rather relaxing: we are allowed to observe the writes happened before us, or any other unordered write (that’s a race). This is a very important property of the model: we specifically allow races, because races happen in the real world. If we forbid races in the model, runtimes would have a hard time optimizing code because they would need to enforce order everywhere.
Notice how that disallows seeing writes ordered after the read in HB order.
The second part puts additional constraint on seeing the preceding writes: we can only see the latest write in happens-before order. Any other write before that is invisible to us. Therefore, in the absence of races, we can only see the latest write in HB.
The consequence of HB consistency is to filter yet another subset of executions which observe something we allow them to observe. HB extends over non-synchronized actions, and therefore lets the model embrace all actions in the executions.
This is what SC-DRF is all about: if we have no races in the program — that is, all reads and writes are ordered either by SO or HB — then the outcome of this program can be explained by some sequentially consistent execution. There is a formal proof for SC-DRF properties, but we will use intuitive understanding as to why this should be true.
Happens-Before: Publication
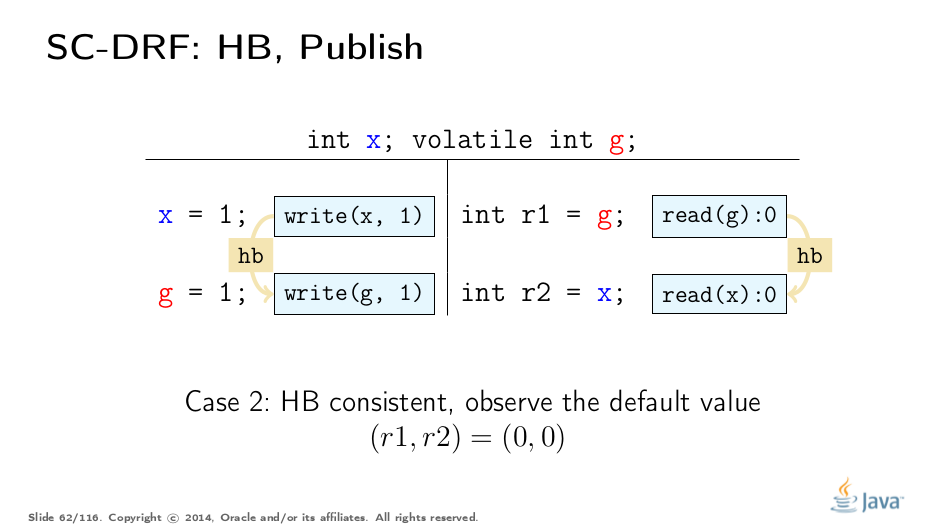
The examples above were rather highbrow, but that is how language spec is defined. Let’s look at the example to understand this more intuitively. Take the same code example, and analyze it with HB consistency rules.
This execution is happens-before consistent: read(x) observes the latest write in HB. The outcome (1, 1) is therefore plausible.
This execution is happens-before consistent, as we read the default value of x. We had omitted the HB edge coming default initialization that synchronizes-with first action in the thread on this chart.
Somewhat surprisingly, the execution with outcome (0, 1) is also happens-before consistent, even though there is no transitive HB between read and write of x. We just read the value via the race — remember the first part in HB consistency definition.
And this execution fails to adhere to HB consistency, and therefore cannot be used to reason about the program outcomes. Therefore this outcome is impossible. Notice that we eliminated (1, 0) from the four of possible outcomes, and that effectively means that we are forced to observe x as 1, if we observed g as 1.
It will hurt our brains to figure out HB orders for real programs, so instead we can derive some simple rules. The source of a synchronizes-with edge is called "release", and the destination is called "acquire". HB contains SW, and therefore, HB spanning different threads also starts at "release", and ends at "acquire".
Release can be thought of as the operation which releases all the preceding state updates into the wild, and acquire is the paired operation which receives those updates. So, after a successful acquire, we can see all the updates preceding the paired release.
Because of the constructions we laid out before, it only works if acquire/release happened on the same variable, and we actually saw the written value. The quiz below further explores this.
Happens-Before: Test Your Understanding
Let’s play a bit more realistically here. Suppose you have the wrapper class which stores ((mail)boxes) some value of type T. Obviously, you have the setter which takes the value, and the getter which returns it. In most programs, reads vastly outnumber writes (otherwise why are you storing the value?), so synchronized getters may become scalability bottlenecks.
People come with their profilers, look at the code and argue: well, it’s just a simple value T, we store it under synchronization, caches are flushed by synchronization, and so we can skip synchronization on read.
Is that true? Answer (select over to reveal): There is certainly a release action on monitor unlock in the setter, but the acquire action is missing in the getter. Therefore, the memory model does not mandate that the values stored before the store to val be visible after we read val in another thread — very bad news if those were the stores into val fields.
Acquire barrier is missing, you say? OK, let us add one, since we "know" the compiler emits one for a volatile read.
Is this broken? If so, why? Answer (select over to reveal): In current practice, it works for a given conservative VM implementation, but JMM-wise, since we don’t do acquire on the same variable as we did the release on, this is not guaranteed. In short, a smarter VM can see you do not use the sinked value, and therefore can pretend we did not see updates to BARRIER, if any, and eliminate it altogether.
This is a correct way to do this. Marking the field volatile provides the release action in the setters, and the paired acquire in the getters. This allows us to relax synchronized in the getters, and leave only the lightweight volatile.
Is synchronized in the setter still required? Answer (select over to reveal): Yes, because the setter requires mutual exclusion: it should set the val only once.
JMM Interpretation: Roach Motel
It may be hard for an optimizing compiler to figure out if a particular optimization breaks the provisions of JMM. Some advanced compilers may construct the memory flows directly. But, basic compiler guys need a set of simple rules to figure out if something is allowed or not. JSR 133 Expert Group created The JSR 133 Cookbook For Compiler Writers to cover this.
It is important to note that the Cookbook is the set of conservative interpretations, not the JMM itself. We will talk briefly about how those interpretations may be derived.
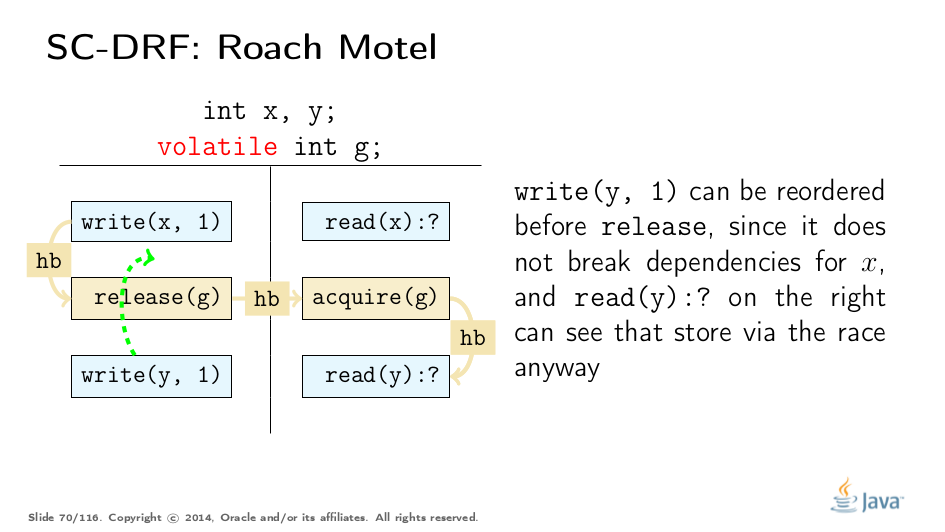
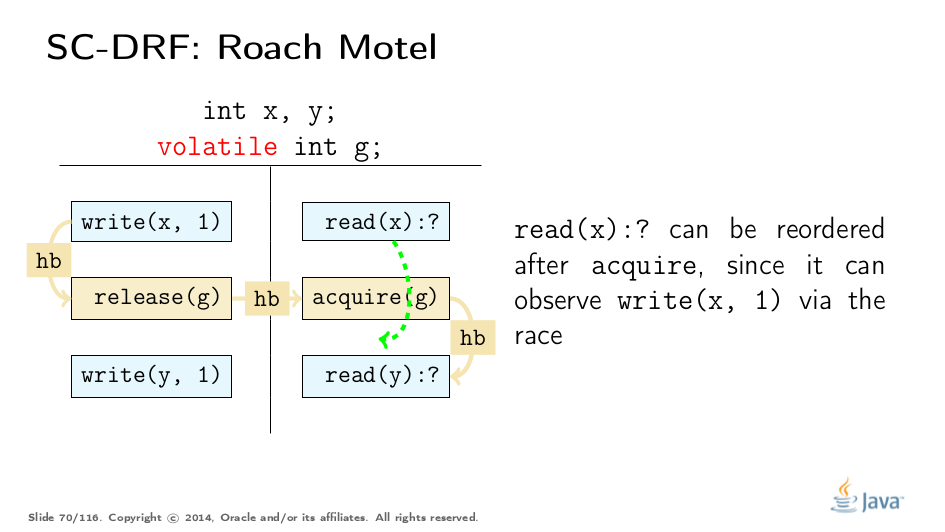
Consider a program, which can be represented by this template execution. The first two types of reorderings are simple:
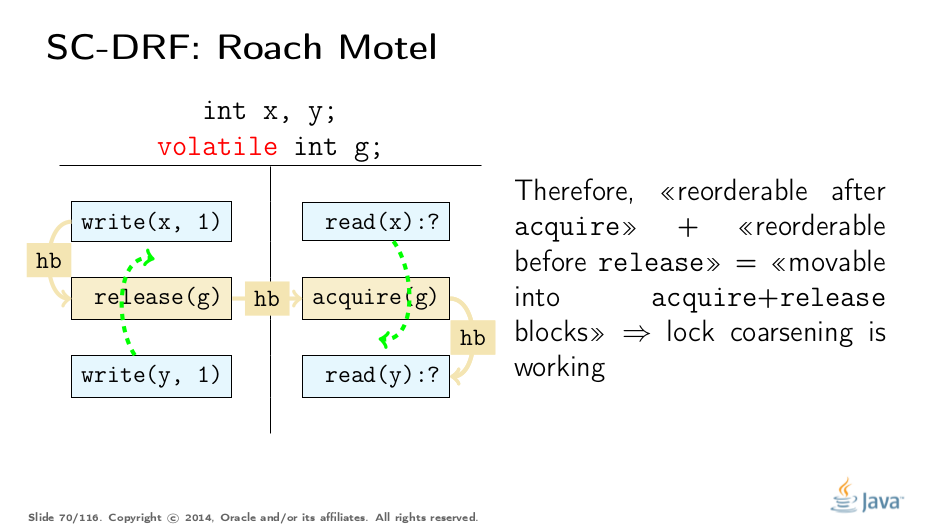
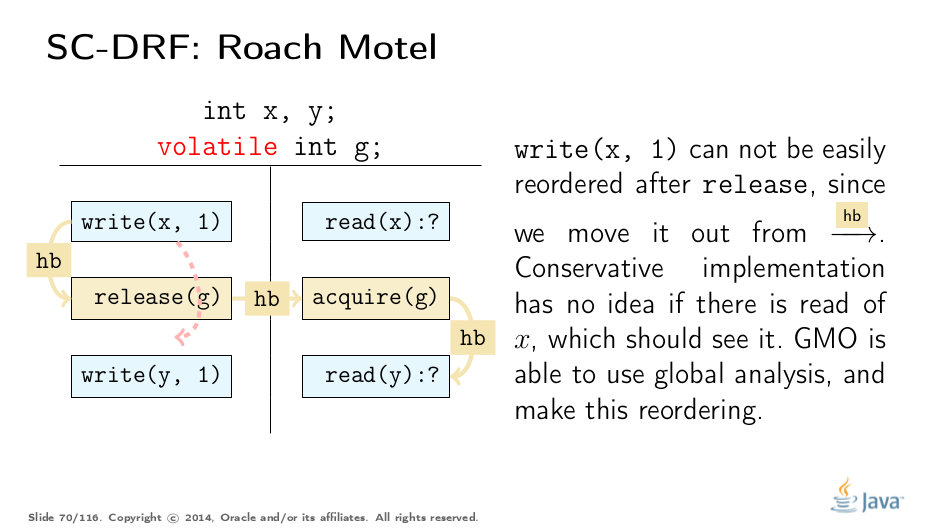
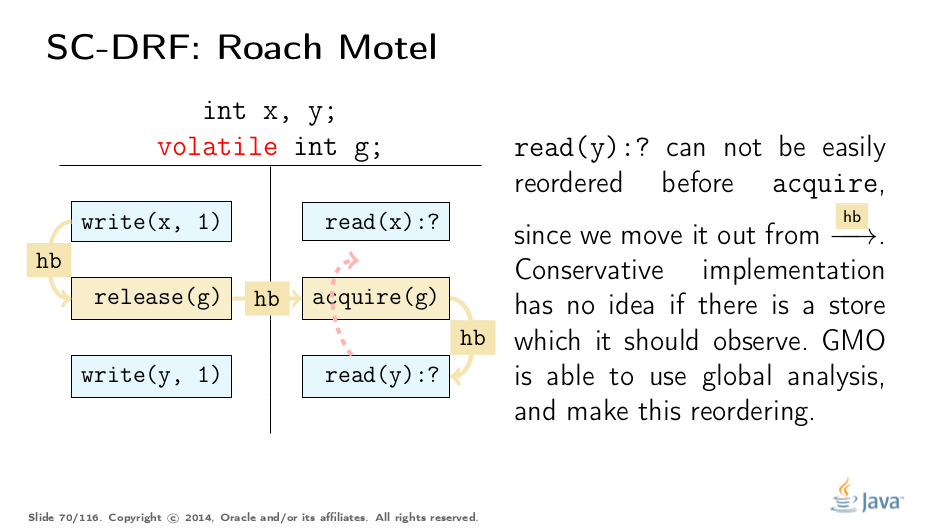
These rules effectively allow pushing the code into the acquire/release blocks, e.g. pushing the code into the locked regions, which enables lock coarsening without violating JMM.
Another two types of reorderings are conservatively forbidden. Note that they are not forbidden by JMM itself, but we have to forbid it if local analysis is not able to determine correctness (in some cases, e.g. field stores in constructors, it can):
Test Your Understanding
Let us try some real examples again.
What can this code print? Answer (select over to reveal): There is a synchronized-with edge between storing of ready, and reading ready==true Therefore, we can see the latest write in the HB order, and that is 42. However, we can also see the out-of-HB (racy) write, and that also brings us 43.
Now we drop volatile.
What can this code print? Answer (select over to reveal): Any value is possible, because we can observe any value via the race, and also we can see nothing at all if while loop is reduced to while(true).
Benchmarks
Of course, what’s the use of me posting anything without benchmarks? We want to quantify at least some of the costs. It does not strike me as a good idea to measure the absolute numbers, and therefore we would only show a few important high-level points. The benchmarks are driven by JMH, and we assume you are familiar with it.
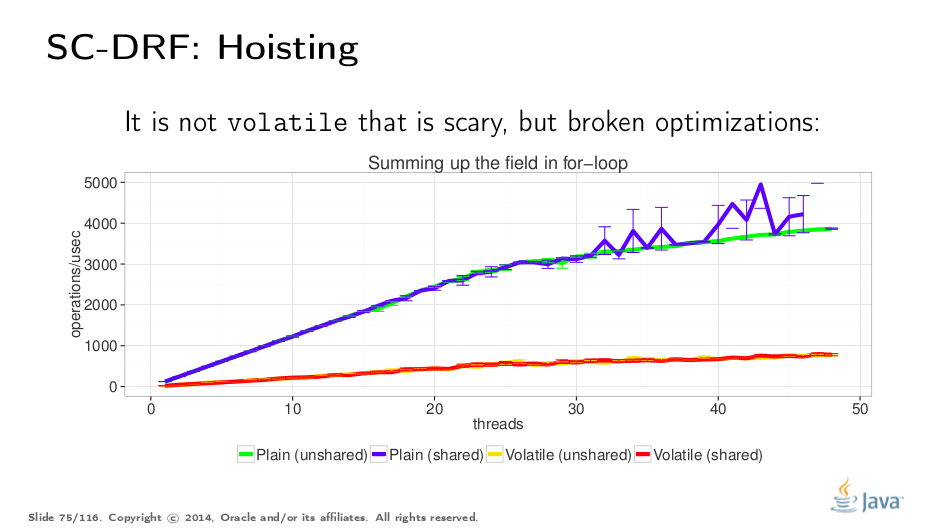
Let us start with a "hoisting" benchmark. We would like to run a synthetic test which naively computes v times v. The difference lies within the sharing of underlying Storage, and v volatility. Not surprisingly, when we are reading stuff, it seems like sharing is not important.
The volatile test cases are significantly slower. However, it is not the cost of volatiles themselves, but rather the evidence of too-conservative implementation breaking the hoisting of s.v out of the loop, which will move the read before the acquire (see the "Roach Motel" above). Pre-reading s.v into a local variable and measuring again is left as an exercise for the reader.
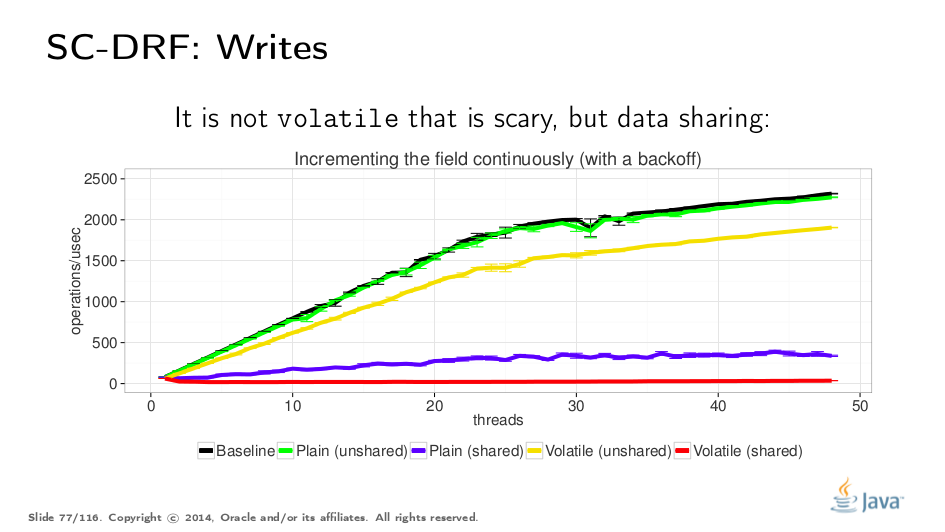
For a writing test, we can start incrementing the same variable. We do a bit of backoff to stop bashing the system with writes, and here we can observe the difference both between shared/unshared cases and between volatile/non-volatile cases. One would expect volatile tests to lose across the board, however we can see the shared tests are losing. This reinforces the idea that data sharing is what you should avoid in the first place, not volatiles.
JMM Updates
Current mainstream languages seem to adopt SC-DRF across the board. However, there is evidence that strictly supporting SC-DRF might not be profitable for all scenarios. For example, Linux RCUs relax some of the constraints with very good performance improvements on weakly-ordered platforms, and arguably do that without breaking usability much.
So the question for the next JMM update is: can/should we relax SC-DRF to get more performance?
Part IV: Out of Thin Air
What Do We Want
It would seem that once SC-DRF is established, we are good to go. Any transformation is valid in between synchronized actions, because if there was an unannotated race in the code, the behavior was non-SC to begin with. Teach runtimes the SC-DRF rules and you are good, right?
What Do We Have
However, this is only part of the truth. Some transformations still break SC. Consider this program: somewhat surprisingly, it is correctly synchronized, since all SC executions have no races, and the only possible result is (0, 0)
Now, an optimizing runtime/hardware comes in and tries to speculate over the branch. It might be a good idea at times to speculatively execute the branch and back off if speculation failed.
Suppose we did this speculation in the code.
Let’s now execute the modified program. The second thread runs unmodified. If we run this program in the order depicted on the slide, we will have (42, 42), because the speculation had turned itself into the self-justifying prophecy! It seems as if 42 came out of thin air.
This example seems artificial, until you realize the variable a could easily be, say, System.securityManager, and we had just undermined platform security guarantees! Scary.
To cover for that, JMM forbids out-of-thin-air (OoTA) values. To constructively forbid OoTA, you need some notion of causality (i.e. "what caused what"), which is tricky to introduce in a model that tries to escape the deadly embrace of global time.
The entire section in JLS 17.4.8 tries to rigorously specify the "commit semantics", which additionally validates the executions for causality violations. We won’t dive into details here, so enjoy this nice Bill-looking guy trying to explain it.
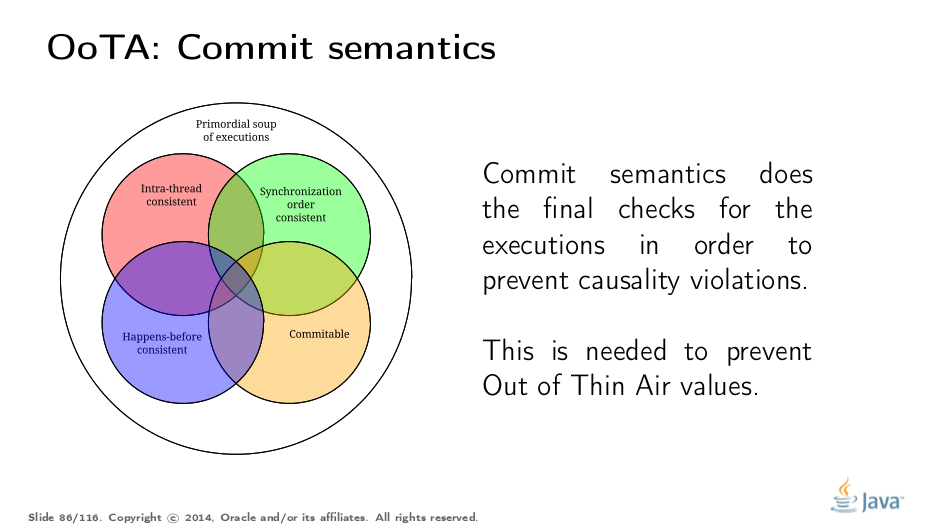
Commit semantics give the last filter in the executions soup. Executions violating the causality requirements cannot be used to reason about the program.
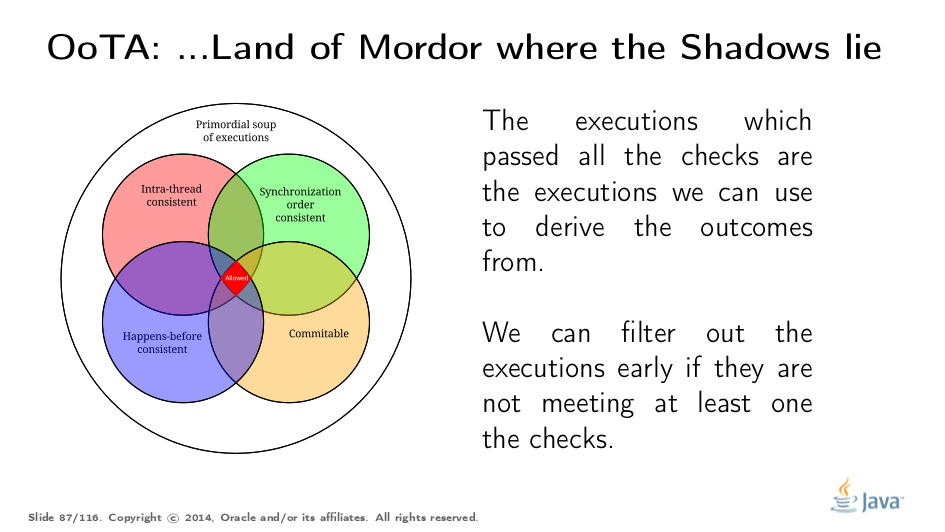
This takes us to the final picture. In order to test if an execution is plausible under JMM, you need to see if it passes all the requirements. Note, however, that you can quickly branch-and-bound the set of considered executions based on the failure of a particular test. In most cases we don’t even get to commit semantics, because all the executions that passed the other filters yield only the desired outcomes, and we don’t care to distinguish between them anymore.
OoTA and C/C++
Remarkably, Java so far seems to be the only platform which tried to specify what OoTA really means. Not that Java is very successful with that, given the very complicated and sometimes counter-intuitive causality model.
JMM Updates
Therefore, in the next JMM update the largest question of all is being asked: can we reformulate/fix this to be more bullet-proof, concise, and understandable?
Part V: Finals
Test Your Basic Understanding
Since we learned a lot about JMM already, let’s start from this simple quiz. What does this program print? Answer (select over to reveal): Nothing, 0, 42, or throws NPE (!). Racy reads abound, and we can really read any value written: either the default one, or that written in constructor. We can even observe first (a != null), and print, only to realize the racy read the second time returned (a == null), setting up an NPE.
What Do We Want
We obviously want to modify the object declaration in such a way that we only get 42 (or nothing). You can guess what hides under five question marks there, right?
We need this to protect ourselves from races. We cannot afford to catch fire and break object invariants if an object receiver acts maliciously — otherwise we can’t write secure code.
Nowadays, some brave folks dance around the races trying to optimize performance. Go read Hans again, please.
What Do We Have
Final fields are remarkably simple to implement, compared to how we need to spec them. On most architectures, it is enough to put a memory barrier at the end of the constructor, and tie the load of object fields via the dependency to the load of original reference. Done.
The specification, however, gets rather complicated. We have to reference the constructors in an otherwise syntax-oblivious spec, and introduce special freeze actions at the end of constructor. Intuitively, this freeze action "sticks" the field with the values initialized in constructors. It does not, however, limit the fields from being modifiable (you can still circumvent finality through Reflection), freeze is only about the initializing stores.
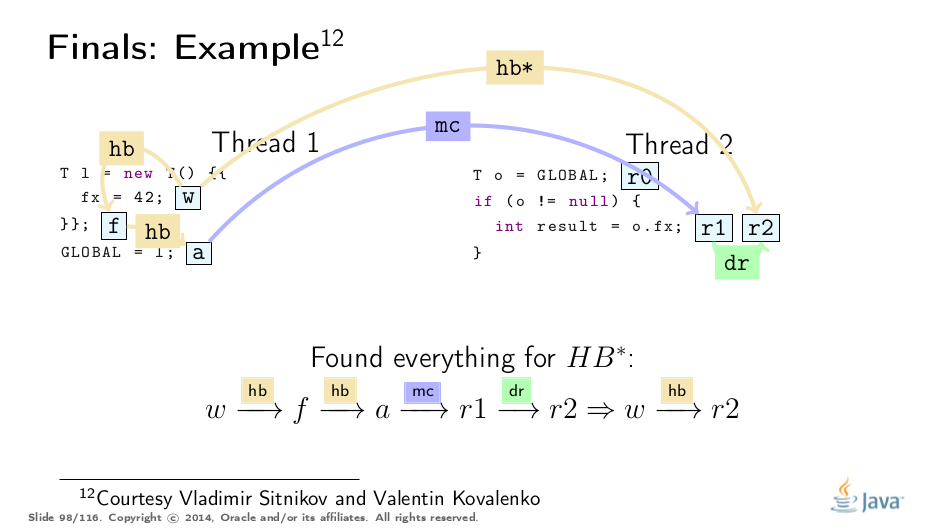
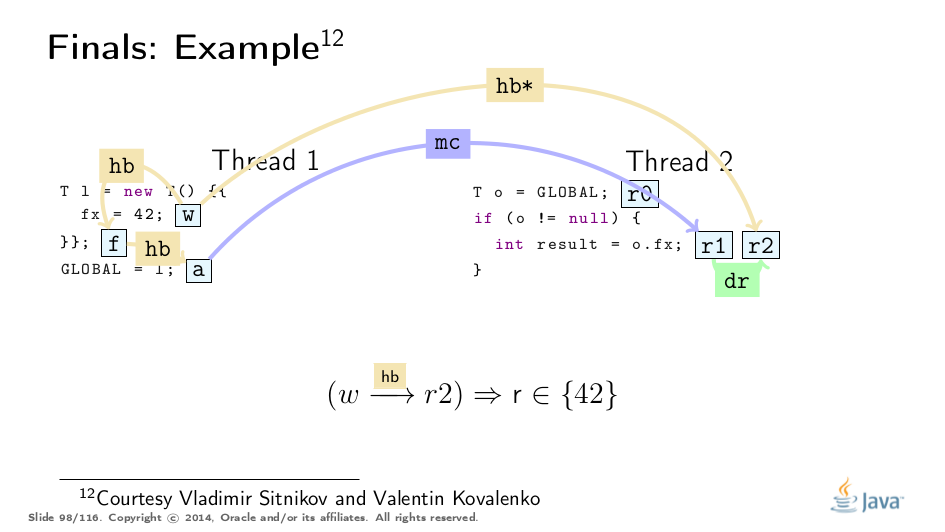
And here is how it is formally specified. Notice that w and r2 may or may not be the write and the read of the final field, they might as well be the write and read of the ordinary, non-final field. What really matters is that the subchain containing freeze action F, some action a, and r1 which reads the final field — all together make r2 observe w.
Notice two new orders, dereference order, and memory order are needed to qualify how frozen values propagate.
We "only" need to make sure that all paths from a target read lead up to a write of frozen value via F and the final field read.
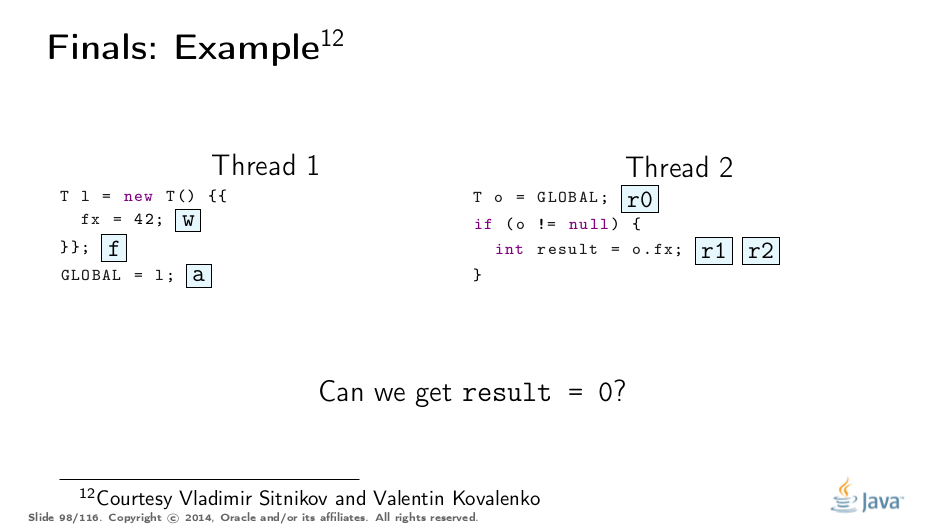
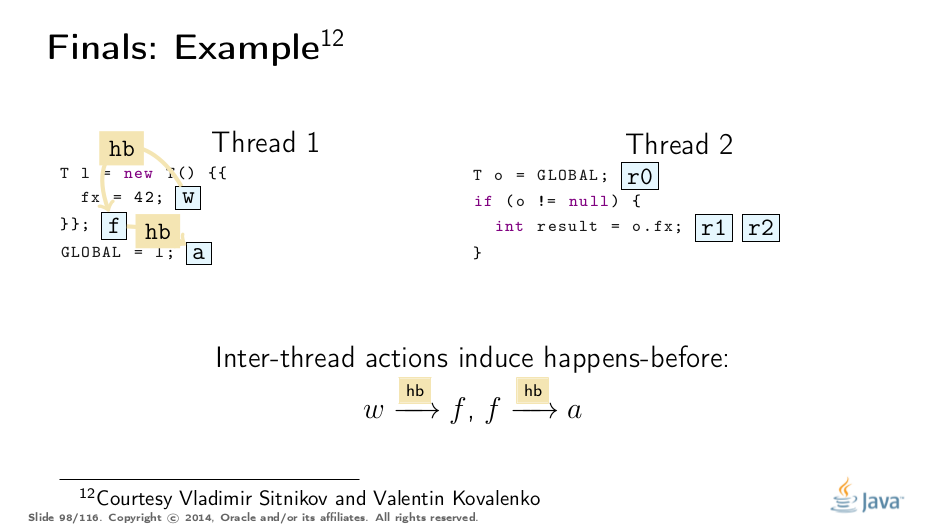
Constructive Example
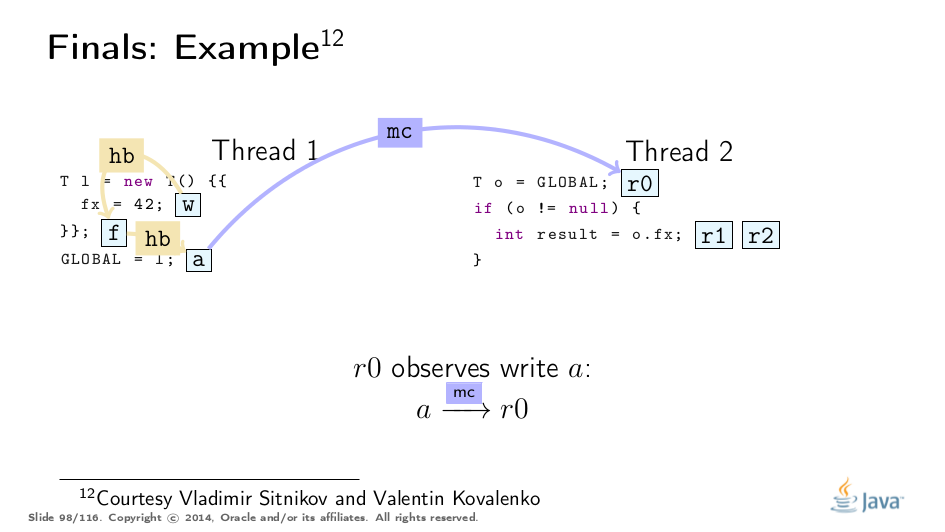
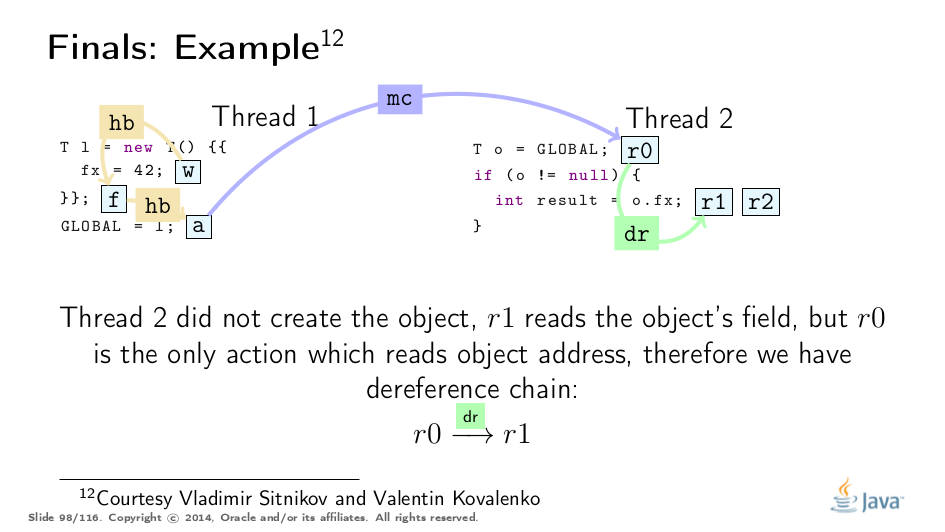
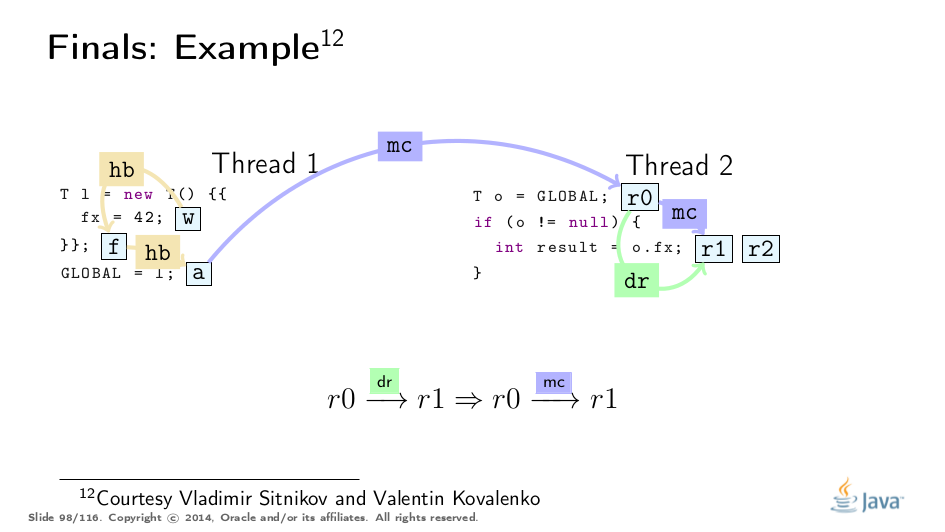
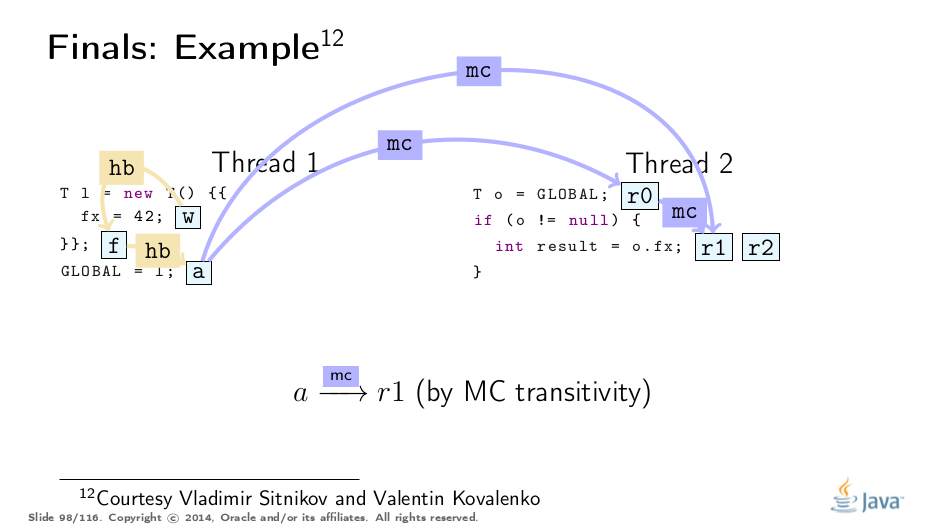
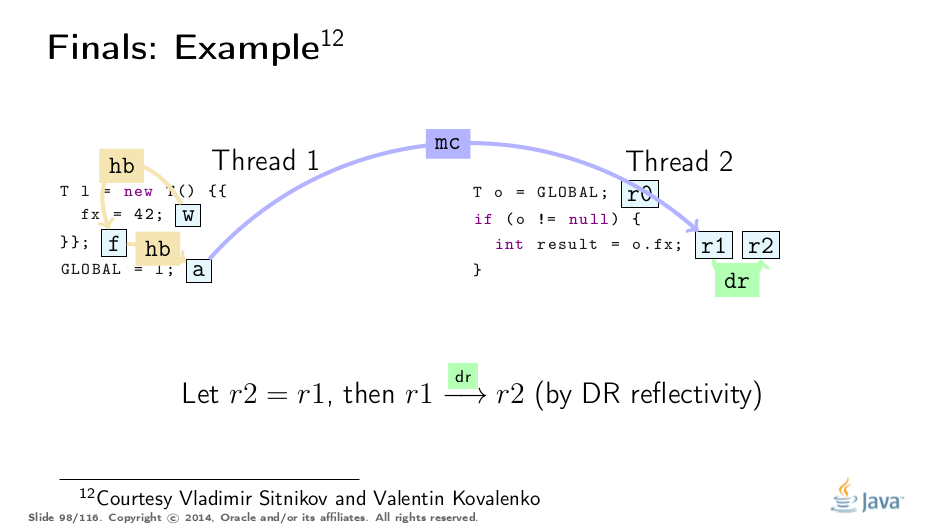
This example was greatly untangled by Vladimir Sitnikov and Vladimir Kovalenko, kudos to them! Here is a visualization based on their analysis:
Premature Publication
This is a great example from Jeremy Manson’s PoPL paper. There, the first thread initializes the object and stores 42 to final field f, then "leaks" the object reference through p, and only then properly publishes via q.
Conventional wisdom suggests that final field guarantees evaporate with premature publication, but really, the third thread only observes the fully-constructed object, and we can find only the proper final path. (See the example above for analogy.)
The second thread, however, breaks out of the final path when reading through p, and therefore may observe non-frozen value. It is somewhat surprising that the read through q can also observe the non-frozen value. This is formally allowed by the properties of dr and mc orders, and has a pragmatic reason:
The pragmatic reason is that runtimes may cache final fields once they discover one! Which means that if the compiler discovered p and q are aliasing the same object, then we can say r3 = r2, and be done with it. So, if we observed the under-constructed object, our thread became tainted, and all hell broke loose.
Test Your Understanding (tricky)
Notice that the spec talks about initializations in constructors, and here we have something else. Answer (select over to reveal): Of course, we will see either 42, or nothing. Field initializers and instance initializers fire in the course of instance initialization, and arguably are part of constructor.
JMM Updates
There are quite a few problems with final-s, mostly with its orthogonality with regard to other JMM elements. It is particularly interesting how to achieve visibility for initializing stores in a constructor if the field is already volatile. (Hint: volatile is not enough as it stands in spec, at this point).
It is also interesting, from a pedagogical standpoint, whether we should ostracize users who forget to declare their write-once-in-constructor fields final, and get their code to blow up on non-x86 platforms.
Therefore, the next JMM update needs to decide whether we should extend the final field guarantees to all fields initialized in all constructors.
Benchmarks
This section covers the final field considerations for the updated Java Memory Model. See the more-thorough explanation in a separate post.
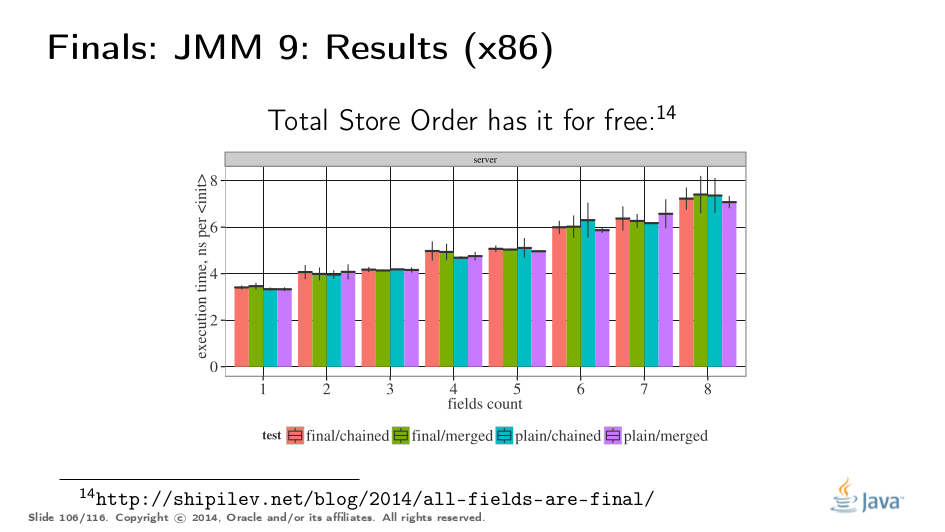
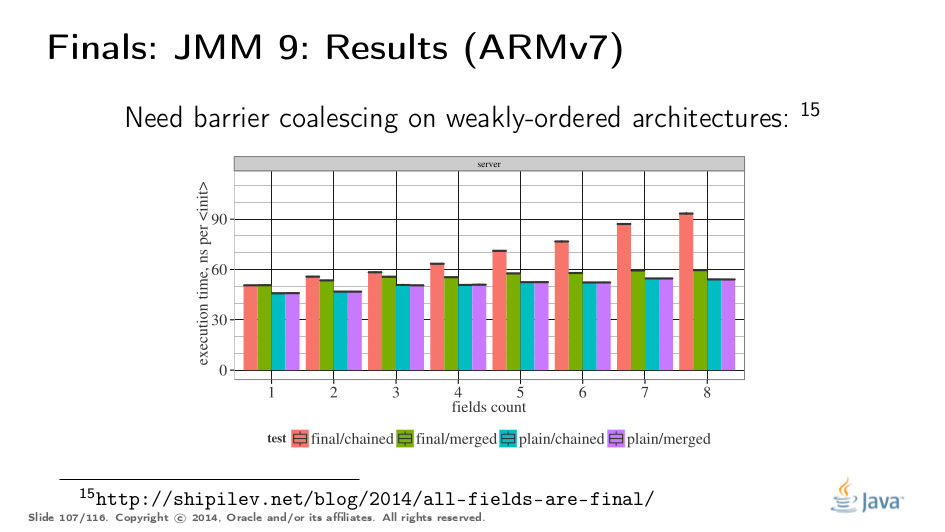
Of course, we would like to rigorously quantify what would it cost to mark all fields final. Since final field stores require memory barriers in the constructors for weakly ordered platforms, we also take the ARM host as a testing platform.
Here are the benchmarks: chained call N constructors up the hierarchy, initializing a single field per class, and merged initialize all N fields at once. Fields can be plain or final. We test with different N-s to see if performance changes in a sane manner.
x86, being a Total Store Order machine, does not have memory barriers, and so the difference between all four variants is within the measurement error, regardless of N.
On weakly-ordered machines, final involves a real memory barrier, and the barrier cost is clearly visible in the addition in execution time on the green bar. Moreover, we have barriers in each superclass, which explain why it takes linearly more time for the red bar. We can teach the VM to merge the barriers though, after which the cost of enforcing the final semantics would drown in allocation costs.
Conclusion
When we were dealing with a nasty JMM bug, Doug dropped a gem of wisdom that should sum up this talk nicely. It would also be good if people using concurrency constructs were able to figure out why and when those constructs work. Hopefully this talk improved JMM understanding.
There are some known problems we would like to address in JMM…
…which gave rise to the "Java Memory Model update" effort.
At the end of the day, a few useful links for readers:
Phew.