About, Disclaimers, Contacts

"JVM Anatomy Quarks" is the on-going mini-post series, where every post is describing some elementary piece of knowledge about JVM. The name underlines the fact that the single post cannot be taken in isolation, and most pieces described here are going to readily interact with each other.

The post should take about 5-10 minutes to read. As such, it goes deep for only a single topic, a single test, a single benchmark, a single observation. The evidence and discussion here might be anecdotal, not actually reviewed for errors, consistency, writing 'tyle, syntaxtic and semantically errors, duplicates, or also consistency. Use and/or trust this at your own risk.

350

Aleksey Shipilëv, JVM/Performance Geek
Shout out at Twitter: @shipilev; Questions, comments, suggestions: aleksey@shipilev.net

Questions

What happens when we call Object.hashCode without the user-provided hash code? How does System.identityHashCode work? Does it take the object address?

Theory

In Java, every object has equals and hashCode, even if users do not provide one. If user does not provide the override for equals, then == (identity) comparison is used. If user does not provide the override for hashCode, then System.identityHashCode is used to perform the hashcode computation.

The Javadoc for Object.hashCode says:

The general contract of hashCode is:

  • Whenever it is invoked on the same object more than once during an execution of a Java application, the hashCode method must consistently return the same integer, provided no information used in equals comparisons on the object is modified. This integer need not remain consistent from one execution of an application to another execution of the same application.

  • If two objects are equal according to the equals(Object) method, then calling the hashCode method on each of the two objects must produce the same integer result.

  • It is not required that if two objects are unequal according to the equals(java.lang.Object) method, then calling the hashCode method on each of the two objects must produce distinct integer results. However, the programmer should be aware that producing distinct integer results for unequal objects may improve the performance of hash tables.

As much as is reasonably practical, the hashCode method defined by class Object does return distinct integers for distinct objects. (This is typically implemented by converting the internal address of the object into an integer, but this implementation technique is not required by the Java™ programming language.)

Hash codes are supposed to have two properties: a) good distribution, meaning the hash codes for distinct objects are as distinct as practically possible; b) idempotence, meaning having the same hash code for the objects that have the same key object components. Note the latter implies that if object had not changed those key object components, its hash code should not change as well.

It is a frequent source of bugs to change the object in such a way that its hashCode changes after it was used. For example, adding the object to a HashMap as key, then changing its fields so that hashCode mutates as well would lead to surprising behaviors: the object might not be found in the map at all, because internal implementation would look in the "wrong" bucket. Likewise, it is a frequent source of performance anomalies to have badly distributed hash codes, for example returning a constant value.

For user-specified hash code, both properties are achieved by computing it over the set of user-selected fields. With enough variety of fields and field values, it would be well distributed, and by computing it over the unchanged (for example, final) fields we get idempotence. In this case, we don’t need to store the hash code anywhere. Some hash code implementations may choose to cache it in another field, but that is not required.

For identity hash code, there is no guarantee there are fields to compute the hash code from, and even if we have some, then it is unknown how stable those fields actually are. Consider java.lang.Object that does not have fields: what’s its hash code? Two allocated Object-s are pretty much the mirrors of each other: they have the same metadata, they have the same (that is, empty) contents. The only distinct thing about them is their allocated address, but even then there are two troubles. First, addresses have very low entropy, especially coming from a bump-ptr allocator like most Java GCs employ, so it is not well distributed. Second, GC moves the objects, so address is not idempotent.[1] Returning a constant value is a no-go from performance standpoint.

So, current implementations compute the identity hash code from the internal PRNG ("good distribution"), and store it for every object ("idempotence").

To achieve this, Hotspot JVM has a few different styles of identity hashcode generators and it stores the computed identity hashcode in the object header for stability. The choice of the identity hashcode generator has direct impact on the the performance of hashCode itself and the hashCode users, notably java.util.HashMap. The implementation choice to store the computed identity hashcode in the object header directly impacts the hashcode accuracy (how many bits we can store), and the complex interaction with other users of the object headers.

There is a place in Hotspot codebase where the hashcode is generated:

static inline intptr_t get_next_hash(Thread* current, oop obj) {
  ...
  if (hashCode == 0) {
    // Use os::random();
  } else if (hashCode == 1) {
    // Use address with some mangling
  } else if (hashCode == 2) {
    // Use constant 1
  } else if (hashCode == 3) {
    // Use global counter
  } else if (hashCode == 4) {
    // Use raw address
  } else {
    // Use thread-local PRNG
  }
  ...
}

This setting it accessible as -XX:hashCode VM option.

The generated hashcode would be installed into object header in ObjectSynchronizer::FastHashCode later, and reused on next hash code requests.

Can we see how it works in practice?

Hashcode Storage

We can look into the identity hash code storage with JOL. In fact, there is a JOLSample_15_IdentityHashCode sample that already captures what we want:

$ java -cp jol-samples/target/jol-samples.jar org.openjdk.jol.samples.JOLSample_15_IdentityHashCode
...

**** Fresh object
org.openjdk.jol.samples.JOLSample_15_IdentityHashCode$A object internals:
OFF  SZ  DESCRIPTION             VALUE
  0   8  (object header: mark)   0x0000000000000001 (non-biasable; age: 0)
  8   4  (object header: class)  0x00cc4000
 12   4  (object alignment gap)
Instance size: 16 bytes
Space losses: 0 bytes internal + 4 bytes external = 4 bytes total

hashCode: 4e9ba398

**** After identityHashCode()
org.openjdk.jol.samples.JOLSample_15_IdentityHashCode$A object internals:
OFF  SZ  DESCRIPTION             VALUE
  0   8  (object header: mark)   0x0000004e9ba39801 (hash: 0x4e9ba398; age: 0)
  8   4  (object header: class)  0x00cc4000
 12   4  (object alignment gap)
Instance size: 16 bytes
Space losses: 0 bytes internal + 4 bytes external = 4 bytes total

Here, the internal generator figured out the hashcode for this object is 4e9ba398, and it recorded it as such in the object header. Every subsequent call for identity hashcode would now reuse this value.

Hashcode Generators Randomness

In order to estimate the randomness of identity hash code generators, we can use the test like this:

public class HashCodeValues {
  static long sink;
  public static void main(String... args) {
    for (int t = 0; t < 100000; t++) {
      for (int c = 0; c < 1000; c++) {
         sink = new Object().hashCode();
      }
      System.out.println(new Object().hashCode());
    }
  }
}

The goal for this test is to print the identity hash codes for consequtive objects. It comes with the demonstration problem: some generators are distributed in appalingly bad way, so on large graph scales they would be indistinguishable from each other. Therefore, the test skips printing the hashcode for the majority of intermediate objects, while still (awkwardly) making sure the hashcode is computed.

The heatmap of hash code values would be something like this:

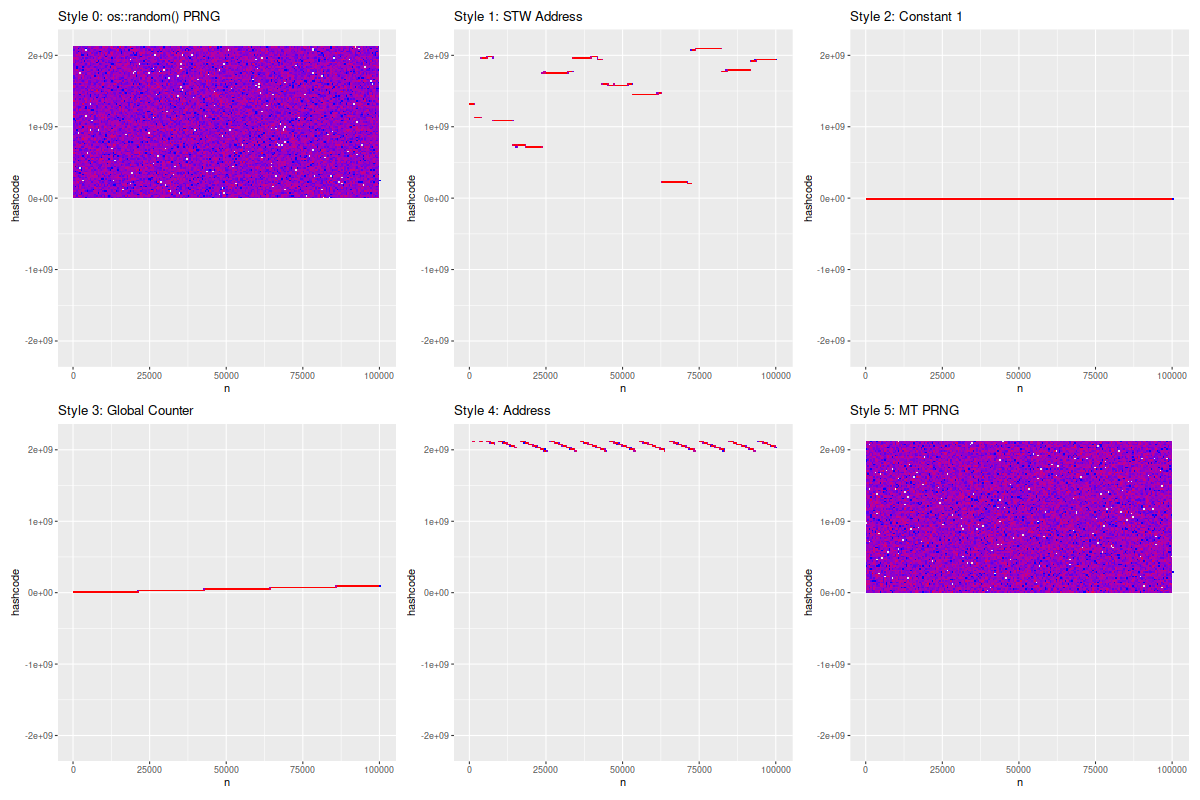
ihc values

Note a few things here:

  1. Both PRNGs have the apparent value domain of nearly half of all possible hashcode values. Only the "upper" half is present in values, because only the first 31 bits of identity hash code is stored in the header in 64-bit JVMs.[2]

  2. The entropy of object addresses is very low. This is due to linear nature of (T)LAB allocations: the temporaly-adjacent objects would have the very similar addresses. Indeed, this is why generating the hashcode from the object address is a bad idea!

  3. Global counters are inconveniently distributed. Thir value domain for global counter is only the number of objects we have ever computed the hashcode for.

  4. Not surprisingly, constant hashcodes exhibit apallingly bad distribution.

The frequently overlooked bit for both address-based and global counter hashcodes is that — while they can be more distinct than PRNGs (which additionally suffer from birthday paradoxes) — they are very well correlated bit-wise, which runs into the risk of getting a sub-hash collision once you select the non-lower-bit subruns from the hash code. Additionally, regular hashcodes like the global counter ones perform oddly when we deal with elements in a regular pattern, for example, retaining every second object in the hash table quickly leads to having the elements with only odd/even hashcodes, which underutilizes the hash tables doing e.g. hashcode % size bucket placement.

Hashcode Generators Performance

It might be fun to see what performance you can get from these generators. In a simple JMH benchmark like this, you have more or less predictable results:

@Warmup(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@Measurement(iterations = 5, time = 1, timeUnit = TimeUnit.SECONDS)
@Fork(3)
@Threads(Threads.MAX)
@OutputTimeUnit(TimeUnit.NANOSECONDS)
@BenchmarkMode(Mode.AverageTime)
@State(Scope.Benchmark)
public class IdentityHashCode {
    Object o = new Object();

    @Benchmark
    public void cold(Blackhole bh) {
        Object lo = new Object();
        bh.consume(lo);
        bh.consume(lo.hashCode());
    }

    @Benchmark
    public void warm(Blackhole bh) {
        Object lo = o;
        bh.consume(lo); // for symmetry
        bh.consume(lo.hashCode());
    }
}

On a small ultrabook with latest JDK 17 EA, it would yield:

Benchmark              Mode  Cnt    Score   Error  Units

# Style 0: os::random() PRNG
IdentityHashCode.cold  avgt   15  400.703 ± 12.470  ns/op
IdentityHashCode.warm  avgt   15    5.051 ±  0.064  ns/op

# Style 1: STW Address
IdentityHashCode.cold  avgt   15   86.180 ±  1.854  ns/op
IdentityHashCode.warm  avgt   15    5.109 ±  0.074  ns/op

# Style 2: Constant 1
IdentityHashCode.cold  avgt   15   83.195 ±  2.034  ns/op
IdentityHashCode.warm  avgt   15    5.045 ±  0.060  ns/op

# Style 3: Global Counter
IdentityHashCode.cold  avgt   15  124.748 ±  0.946  ns/op
IdentityHashCode.warm  avgt   15    5.069 ±  0.079  ns/op

# Style 4: Address
IdentityHashCode.cold  avgt   15   86.232 ±  2.984  ns/op
IdentityHashCode.warm  avgt   15    5.066 ±  0.058  ns/op

# Style 5: MT PRNG
IdentityHashCode.cold  avgt   15   90.809 ±  0.792  ns/op
IdentityHashCode.warm  avgt   15    5.087 ±  0.077  ns/op

Note a few things:

  1. The warm variants perform the same, regardless of the generator used. This makes sense, as that path only picks up already stored identity hash code.

  2. The majority of the cold cost is going to VM for hash code calculation. Even the most basic generator that returns a constant 1 costs quite a lot.

  3. Other generators snowball with their own effects. Notably, os::random() PRNG does the atomic updated to the PRNG state, and thus suffers from the major scalability problem.

Conclusion

The choice of identity hash code generator is heavily implementation specific. The generator should be both well-distributed and highly scalable. That is why modern Hotspot VMs default to hashCode=5, the multi-threaded PRNGs.[3]

There is no address computation involved in identity hashcode calculation at all. That is one of the reasons why the confusing mention of address computation was finally removed from the Javadoc.[4]

1. Note this is not a problem for the reference comparisons with ==. In the overwhelming majority of VM implementations, reference equality compares addresses. This is mostly because even if GC moves the objects, the Java/runtime code sees the consistent addresses for a given object. If object A had moved, then all references to A are updated to new address "at the same time", either due to stop-the-world GC, or with the help of GC barriers.
2. It is even worse for 32-bit VMs, that store only the first 25 bits, see more discussion about it here.
3. Somewhat amuzingly, I have accidentally changed it from 0 to 5 after doing the performance experiments for JDK-8006176. This process mistake still haunts me.
4. See JDK-8199394.